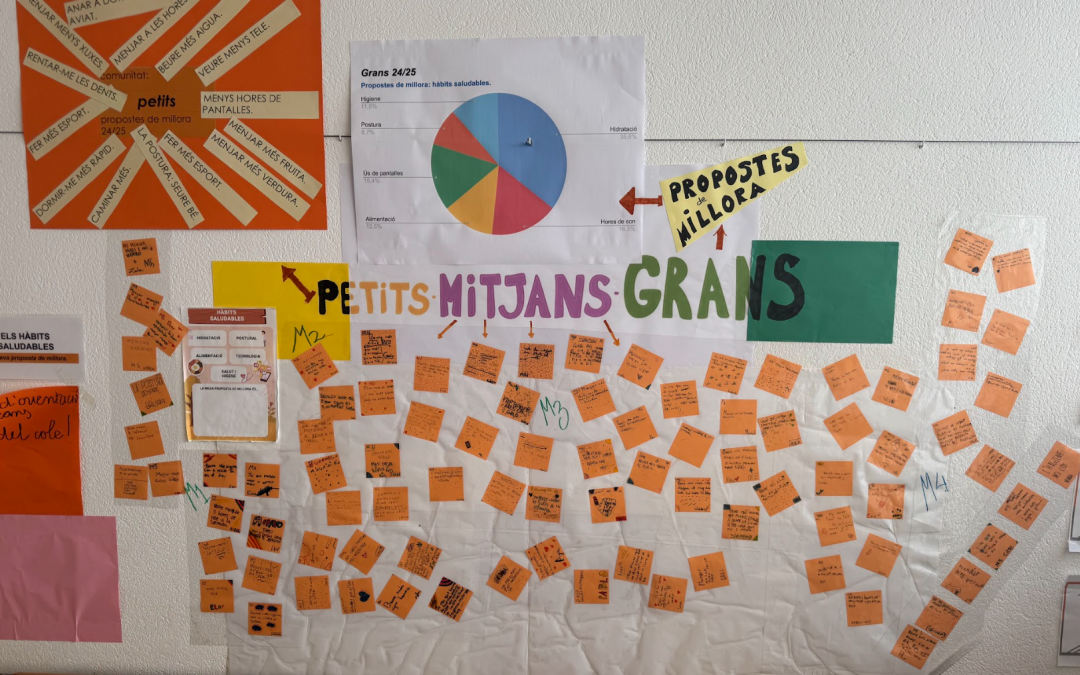
Situacions d’aprenentatge:
A l’escola un dels aspectes que treballem en el “Saber estar” és l’ordre. Entenem l’ordre no només com una qüestió d’organització, sinó com una oportunitat d’aprenentatge. És per això que cada inici de curs, a totes les comunitats —des d’I3 fins a 6è— plantegem el repte de com organitzar els calaixets personals. Lluny de ser una tasca automàtica, convertim aquesta situació quotidiana en un escenari d’aprenentatge, una indagació col·lectiva rica i significativa, amb un component matemàtic i relacional.
A la comunitat de mitjans, aquesta proposta es va decidir vincular-la a les matemàtiques del nostre cos. A continuació, compartim l’experiència viscuda a l’aula de Mitjans 2, pas a pas, des del misteri inicial fins a la descoberta col·lectiva del propi lloc. A mesura que aneu llegint, us adonareu que l’ordenació dels calaixets es va convertir en un projecte que va posar en joc les matemàtiques, la capacitat d’observació, el pensament crític i la comunicació.
Provocació: un misteri a l’aula
Tot va començar un matí en què els infants van trobar un objecte nou a l’aula: una bàscula.
Evocació: setmanes anteriors
De seguida, la seva presència va despertar la curiositat i van començar a emergir hipòtesis relacionant-les amb la idea que dies enrere havíem parlat de començar l’activitat dels calaixets:
- “Jo crec que per resoldre això hem de fer servir l’eina (rutina de pensament) que vam utilitzar la setmana anterior “ Jo veig, jo penso i jo em pregunto”.
- “Jo veig… una bàscula.”
- “Jo penso que la bàscula podria tenir alguna relació amb l’ordre dels calaixets.”
- “Jo em pregunto si potser, qui pesa més, li tocarà el calaixet de sota?”
- “Jo penso que potser la bàscula ens servirà per saber qui és més alt…”
Aquestes primeres idees van donar lloc a converses espontànies carregades de sentit:
- Però si volem saber l’alçada… per què cal una bàscula?
- La bàscula és per saber el pes, no l’alçada!
- Aleshores, per mesurar l’alçada, potser caldria un metre!
- Sí, perquè cada eina serveix per mesurar coses diferents!
Aquest tipus d’intercanvis van permetre abordar nocions importants com la funció de les eines de mesura, les diferències entre magnituds i, sobretot, la legitimitat de totes les idees com a motor del pensament entenent l’escola com un espai segur on compartir idees i reflexions. Davant d’un comentari que qüestionava una aportació, la mestra va obrir un espai per parlar sobre l’error com a font de descobriment i sobre la importància de compartir pensaments sense por de ser jutjats:
“Si no ens equivoquem, potser no trobarem mai coses noves…”
“A vegades, quan un s’equivoca, descobreix alguna cosa genial!”
Després de la reflexió es va convidar l’alumne a tornar a intervenir de manera constructiva, amb un feedback positiu:
- Jo penso que l’alçada i la bàscula no tenen relació, no m’encaixen. La bàscula és per mesurar el pes i no l’alçada.
Coneixements previs: Connectant amb el que sabem
Per reprendre el fil d’anys anteriors, la mestra va preguntar:
- De quines maneres heu ordenat els calaixets altres anys?
- Per l’alçada!
- Pel pes!
- Pel nombre de lletres del nom!
- Per qui viu més a prop de l’escola!
- Pel salt de llargada!
- Pel dia que vam néixer!
Aquest record col·lectiu va permetre reconèixer la riquesa de criteris possibles i va donar peu a la nova proposta: crear una fórmula matemàtica a partir de dades del nostre cos. Primer de tot vam partir dels coneixements previs tot preguntant si sabien què era una fórmula:
- Una fórmula és una cosa que li poses coses i surt una altra cosa.
- És com una contrasenya!
- O com una poció, que té ingredients i un ordre per fer-la.
Entre totes les aportacions, vam crear la definició compartida:
“Una fórmula és un patró de números i lletres combinats en un ordre concret per trobar un resultat.”
Creant fórmules i recollint dades debatem estratègies
Cada grup va inventar la seva pròpia fórmula composta per cinc dades (D1 a D5). Vam parlar d’operacions:
– Podem sumar, restar, dividir i multiplicar!
– També podem ajuntar: per exemple, 3 i 5 fan 35!
– Però ajuntar no és sumar? 3+5 fan 8!
– Nom ajuntar vol dir posar-los al costat de l’altre!
– Jo crec que aleshores vols dir 30 + 5!

Per decidir les dades, vam fer pluja d’idees amb el criteri que no podien repetir-se estratègies de cursos anteriors:
– Podem fer servir el perímetre del cap!
– Quants segons triguem a córrer una distància.
– La mida del peu!
– Els òrgans es poden mesurar?
– Podem recollir dades de si el cor ens va més de pressa o més lent quan estem cansats?, perquè jo quan corro el cor em va a mil!
– Podem saber si tenim molt d’aire als pulmons?
– Tots tenim les mateixes dents?
Algunes dades van obrir nous interrogants:
– I amb què es mesuren els pulmons i el cor?
– Ho podríem preguntar a un metge/metgessa!
– La meva mare és metgessa, li podem escriure un correu!



Aquest procés va requerir consensuar què volíem mesurar, quines eines utilitzaríem i amb quines unitats ho faríem. Com que moltes de les eines necessàries per recollir les dades —i fins i tot algunes unitats— no estaven al nostre abast, vam decidir demanar suport a la comunitat, especialment a les famílies, mitjançant el correu electrònic.


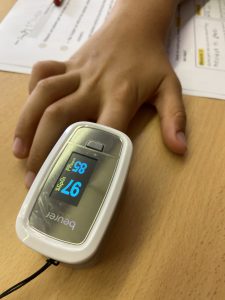

Un cop recollides totes les dades amb les eines adequades, vam començar a fer càlculs amb els resultats, les converses no deixaven de generar nous aprenentatges:
– M’ha sortit un decimal i no sé sumar amb comes!
– Ho pots arrodonir!
– Què vol dir arrodonir?
– Mira, el teu número és 18,9, què està més a prop del 18 o del 19?
– Del 19!
– Doncs ja saps arrodonir!
– I si és 18.5, la ratlleta llarga de la cinta està al mig dels dos números!
– La ratlleta llarga vol dir que estàs al mig, aleshores jo crec que arrodonim cap al número més gran.

Aquestes discussions van evidenciar processos reals de pensament matemàtic, en què es debatien estratègies, s’argumentava i es buscava consens.
Va ser una gran oportunitat per parlar, de manera significativa, parint d’una experiència, de nombres decimals, comparació, aproximacions i criteris.
Finalment, cada infant va tenir el seu resultat numèric. Ara, ja teníem, un número, però encara no sabíem com repartir-nos els calaixets.
De la dada a l’espai
Amb aquestes noves eines, els infants estaven preparats per resoldre l’últim misteri: els calaixets ara tenien una cinta en forma d’eixos i a l’eix horitzontal hi havia números i en el vertical hi havia lletres. Era com una coordenada, però només teníem un número relacionat amb la fórmula… d’on trauríem la lletra?
– Això és com el joc d’Hundir la flota!
– Ens serveix per dir-nos on està cada cosa!
Això va donar peu a treballar les coordenades cartesianes i la seva aplicació a l’aula:
– Si jo tinc A5, m’haig de col·locar on la lletra A i el número 5 es creuen!
– És com llegir un mapa!
– Primer va el número o la lletra?
– Primer el de baix, després el de dalt… o sigui, (5,A)!
Cada infant va trobar de manera aleatòria unes coordenades en un full a sobre de la taula.


– Jo tinc punts, però no sé per què volem això?
– Jo tinc un llibre a casa que si ajuntes tots els punts et surt un dibuix… ho provaré!
– M’ha sortit una lletra C!
– A mi també!
– Doncs a mi una B!
– I ara què fem?
– I si tots els que tenim una C ens ajuntem i ens fixem en el número que ens va sortir a la fórmula?
Aquest darrer debat va portar a parlar de criteris d’ordenació i simbolisme matemàtic. Cada grup va decidir si volia ordenar de petit a gran o a l’inrevés, i ho van anotar en una graella per practicar l’ús dels signes < i >.
– El 35 és més gran que el 31?
– Sí, perquè el 3 el tenen igual, però l’u és més petit que el cinc!
– Això ho podem apuntar amb aquest símbol: >
Així, de manera autònoma i significativa, tothom va trobar el seu lloc dins l’espai compartit.
Metacognició: Un lloc per a cadascú, construït entre tots
El projecte es va tancar amb la col·locació final dels noms als calaixets. Cadascú va trobar el seu lloc a partir d’un procés que havia estat compartit, sentit i construït en col·laboració. Tothom havia aportat idees, resolt dubtes, escoltat altres punts de vista i celebrat els descobriments.

Aquesta experiència ha anat molt més enllà d’una activitat matemàtica. Ha estat una oportunitat per observar, pensar, proposar, equivocar-se, escoltar i construir conjuntament, Les converses espontànies, els debats, les estratègies i les connexions dels infants han estat el motor d’aprenentatge i han permès que se sentissin els protagonistes d’una gran aventura. Una mostra viva de com es pot construir coneixement des del cos, la conversa i la vivència compartida.
– Ara sí que entenc què és una fórmula, perquè n’he inventat una!
– M’ha agradat poder decidir amb el meu grup com ordenar-nos!
– Jo pensava que era impossible sumar amb decimals!, de moment arrodonir m’ha ajudat!
– M’ha encantat poder trobar misteris misteriosos perquè feia que vingués i marxés de l’escola molt emocionada!
Quan escoltem realment els infants, els aprenentatges esdevenen significatius, transferibles, funcionals, productius i memorables.